Didattica di Scienze

Eratostene di Cirene
(Cirene, c. 275 p.e.v. – Alessandria d'Egitto, c. 195 p.e.v.)

E' stato un matematico, astronomo, geografo e poeta greco antico, uno degli intellettuali più versatili della sua epoca: terzo bibliotecario della Biblioteca di Alessandria e precettore di Tolomeo IV, è oggi ricordato soprattutto per aver misurato per primo con grande precisione le dimensioni della Terra. Fu proprio Eratostene ad introdurre il termine Geografia con il significato di descrizione della Terra.
Ma è la misura del meridiano terrestre il risultato più famoso di Eratostene. Stimò per esso una lunghezza di 252.000 stadi, con un errore, tra il -2,4% e il +0,8% rispetto al valore corretto. Il procedimento seguito era descritto in un'opera (perduta) in due libri "Sulla misura della Terra"; ad essere pervenuto è un breve resoconto divulgativo e semplificativo fatto da Cleomede nella sua unica opera pervenuta a noi "De motu Circulari Corporum Caelestium".

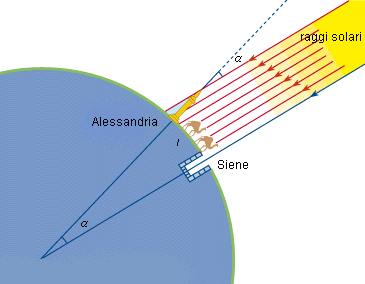
Eratostene sapeva che a Siene (l'attuale città di Assuan, che si trova a circa 800 Km a sud-est di Alessandria), in un momento preciso dell'anno, il sole illuminava il fondo dei pozzi. Questo evento si ripeteva ogni anno a mezzogiorno del solstizio d'estate e dipendeva dal fatto che i raggi del sole cadevano verticalmente. In quel momento, un bastoncino piantato verticalmente a terra non avrebbe proiettato nessuna ombra. Egli notò che ad Alessandria, dove egli viveva, nello stesso giorno e alla stessa ora i raggi del Sole non erano perpendicolari ma formavano un angolo di 7,2° con la verticale. Per calcolare questi angoli Eratostene usava la scafa, un orologio solare inventato da Aristarco.
Eratostene assunse, correttamente, che la distanza del Sole dalla Terra fosse molto grande e che quindi i suoi raggi fossero praticamente paralleli quando raggiungono la superficie terrestre. Inoltre considerava che la Terra dovesse avere forma sferica.
La differenza di inclinazione di 7,2° dipende dalla curvatura della superficie terrestre che cambia il punto di vista dal quale gli abitanti delle due città vedono il Sole.
Egli ragionò in questo modo: l'angolo di 7,2° è congruente all'angolo che ha per vertice il centro della Terra e i cui lati passano rispettivamente per Alessandria e Siene (infatti arrowsono angoli corrispondenti). Si tratta quindi di una "distanza angolare" tra le due città, pari a un cinquantesimo dell'angolo giro.
Ciò significa anche che la distanza "effettiva" tra le due città (ritenuta di 5.000 stadi) è un cinquantesimo della circonferenza terrestre.
Eratostene moltiplicò per 50 questo valore, ottenendo 250.000 stadi: la prima misura scientifica della circonferenza terrestre. A quel tempo la stima di distanze così grandi, misurate a passi, era sicuramente molto imprecisa; inoltre è molto difficile stabilire una corrispondenza esatta tra lo stadio e il metro attuale. Di conseguenza non è facile determinare con sicurezza il margine di errore dei risultati ottenuti da Eratostene.

Simulazione dell'esperienza di Eratostene

La prima applet java a destra permette di comprendere meglio lo schema geometrico della situazione studiata da Eratostene. Consente infatti di "spostare virtualmente" la posizione di Alessandria rispetto a Siene: basta cliccare su un punto qualsiasi della retta r e, mantenendo premuto il tasto, trascinare il mouse.
Si nota che l'angolo formato dai raggi solari rispetto alla verticale è congruente con l'angolo al centro della Terra. Questo perché i due angoli considerati sono alterni interni, formati da una retta (r) che interseca due rette parallele (i raggi solari). Nel nostro caso, in nessuna delle località di osservazione i raggi del Sole potranno cadere verticalmente. Quindi la situazione geometrica è un po' più complicata.



Simulazione dell'esperienza in due località qualsiasi

La situazione geometrica per due località qualsiasi è invece mostrata nella seconda applet java. Rispetto alla situazione studiata da Eratostene, questa è un po' più complicata: i due punti A e B rappresentano due località qualsiasi che si trovano lungo uno stesso meridiano. In corrispondenza di ognuna di esse è stato disegnato uno gnomone verticale (AQ e BP). I raggi solari non cadono necessariamente verticali in nessuno dei due luoghi. C è il centro della Terra. Le rette r e s sono parallele. L'applet ci consente di "spostare virtualmente" le posizioni reciproche dei punti A e B trascinandoli con il mouse, oppure di modificare l'inclinazione dei raggi solari, trascinando con il mouse la retta s. Si può notare che gli angoli segnati da un solo archetto sono congruenti all'angolo al centro della Terra.
Infatti:
RPS = KBP perché sono opposti al vertice
KBP = C perché sono alterni interni fra due parallele intersecate da una retta.
Inoltre, se gli angoli indicati con tre archetti rappresentano l'inclinazione del Sole rispetto alla verticale del luogo A, e l'angolo RPT quella del luogo B, allora l'angolo al centro della Terra è la differenza tra i due.

Le applet ed i testi sono tratti da http://www.vialattea.net/ ove è ospitata la Rete di Eratostene.